PriorityQueue详解

PriorityQueue详解

PriorityQueue是优先级队列，底层使用数组存储，是基于二叉堆的一个无界队列，可以使用默认排序或者提供Comparator比较器使得队列中的元素有序，入栈出栈的时间复杂度是O(logn)

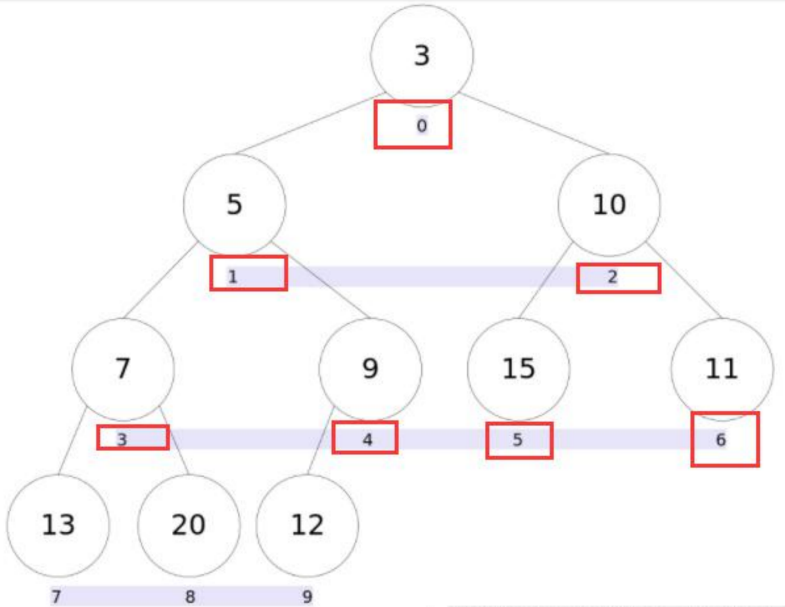
存储结构

堆树的定义

• 是一棵完全二叉树
• 某个节点的值总是不大于或不小于其孩子节点的值
• 每个节点的子树都是堆树

小顶堆

根节点的元素最小是小顶堆(小于左右子节点的值)

graph TD
0((0)) --- 1((1)) --- 3((3))
1((1)) --- 4((4))
0((0)) --- 2((2))

大顶堆

根节点的元素最大是大顶堆(大于左右子节点的值)

graph TD
0((4)) --- 1((3)) --- 3((1))
1((3)) --- 4((0))
0((4)) --- 2((2))

源码分析

是通过数组来存储的堆树，父子节点的下标关系为

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2

重要属性

// 默认的初始容量
private static final int DEFAULT_INITIAL_CAPACITY = 11;

/**
 * 使用数组存放  是一个平衡二叉堆，对于queue[n]有两个子节点queue[2*n+1] 和 queue[2*(n+1)]
 */
transient Object[] queue; // non-private to simplify nested class access

/**
 * 优先队列中的元素个数
 */
private int size = 0;

/**
 * 比较器，如果为null，为使用默认的自然排序
 */
private final Comparator<? super E> comparator;

/**
 * 修改次数
 */
transient int modCount = 0; // non-private to simplify nested class access

/**
* 最大容量
*/
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

构造器

public PriorityQueue() {
    this(DEFAULT_INITIAL_CAPACITY, null);
}

public PriorityQueue(int initialCapacity) {
    this(initialCapacity, null);
}

public PriorityQueue(Comparator<? super E> comparator) {
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

public PriorityQueue(int initialCapacity,
                     Comparator<? super E> comparator) {
    // Note: This restriction of at least one is not actually needed,
    // but continues for 1.5 compatibility
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    this.queue = new Object[initialCapacity];
    this.comparator = comparator;
}

@SuppressWarnings("unchecked")
public PriorityQueue(Collection<? extends E> c) {
    if (c instanceof SortedSet<?>) {
        SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
        this.comparator = (Comparator<? super E>) ss.comparator();
        initElementsFromCollection(ss);
    }
    else if (c instanceof PriorityQueue<?>) {
        PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
        this.comparator = (Comparator<? super E>) pq.comparator();
        initFromPriorityQueue(pq);
    }
    else {
        this.comparator = null;
        initFromCollection(c);
    }
}

@SuppressWarnings("unchecked")
public PriorityQueue(PriorityQueue<? extends E> c) {
    this.comparator = (Comparator<? super E>) c.comparator();
    initFromPriorityQueue(c);
}

@SuppressWarnings("unchecked")
public PriorityQueue(SortedSet<? extends E> c) {
    this.comparator = (Comparator<? super E>) c.comparator();
    initElementsFromCollection(c);
}

常用方法

获取顶端元素

// 直接取数组中的第一个元素就是顶端元素
public E peek() {
    return (size == 0) ? null : (E) queue[0];
}

插入

以使用默认比较器为例

// add方法直接调用offer方法，往数组末尾添加元素
public boolean add(E e) {
    return offer(e);
}

public boolean offer(E e) {
  if (e == null)
    throw new NullPointerException();
  modCount++;
  int i = size;
  // 看一下数组容量是否足够
  if (i >= queue.length) // 不够则扩容
    grow(i + 1);
  size = i + 1;
  if (i == 0) // 首次添加，将元素放到顶端即可
    queue[0] = e;
  else
    siftUp(i, e);
  return true;
}

// 传入的minCapacity为插入该数据所需要的最小容量
private void grow(int minCapacity) {
  int oldCapacity = queue.length;
  // 如果原始容量小于64，则容量加2，否则容量增加50%
  int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                   (oldCapacity + 2) :
                                   (oldCapacity >> 1));
  // overflow-conscious code
  if (newCapacity - MAX_ARRAY_SIZE > 0)
    // 如果扩容之后的容量大于MAX_ARRAY_SIZE,则比较所需要的容量和MAX_ARRAY_SIZE的大小  
    //(minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;
    newCapacity = hugeCapacity(minCapacity);
  queue = Arrays.copyOf(queue, newCapacity);
}

private void siftUp(int k, E x) {
  if (comparator != null) // 使用自定义选择器
    siftUpUsingComparator(k, x);
  else // 使用默认的自然排序，默认的排序为小顶堆
    siftUpComparable(k, x);
}
// 存放数据的核心代码
// k为所要存放的索引位置，x为元素
private void siftUpComparable(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>) x;
  while (k > 0) {
    int parent = (k - 1) >>> 1; // 左移一位找到父节点的位置
    Object e = queue[parent];// 父节点元素
    if (key.compareTo((E) e) >= 0) // 比较该元素和父节点元素大小,如果该节点大，则跳出循环
      break;
    queue[k] = e; // 将父节点的值存到k索引位置
    k = parent; // 索引位置变成父节点的索引位置，继续对比父节点的父节点
  }
  queue[k] = key;
}

添加元素位于末尾，同时队列长度加1，然后这个元素与它的父节点进行比较，如果比父节点小就与父节点进行交换，重复此过程，直到元素大于父节点结束该过程

删除

还是以默认的比较器为例

public boolean remove(Object o) {
      // 找到该对象对应的索引位置
    int i = indexOf(o);
    if (i == -1)
        return false;
    else {
        removeAt(i);
        return true;
    }
}

// 找到该对象对应的索引位置
private int indexOf(Object o) {
  if (o != null) {
    for (int i = 0; i < size; i++)
      if (o.equals(queue[i]))
        return i;
  }
  return -1;
}

private E removeAt(int i) {
  // assert i >= 0 && i < size;
  modCount++;
  int s = --size;
  // 尾结点
  if (s == i) // removed last element
    queue[i] = null;
  else {
    // 尾结点的元素
    E moved = (E) queue[s];
    // 将尾结点置空
    queue[s] = null;
    siftDown(i, moved);
    // 没有进while循环时(表示在siftDown()方法中直接走到queue[k] = key;),删除节点没有子节点，开始向上查找
    // 向上查找的原因是因为可能所删除的节点与尾结点处于不同的子树下
    if (queue[i] == moved) {
      siftUp(i, moved);
      if (queue[i] != moved)
        return moved;
    }
  }
  return null;
}

// k为所要删除的元素位置  x为尾结点元素
private void siftDown(int k, E x) {
  if (comparator != null)
    siftDownUsingComparator(k, x);
  else
    siftDownComparable(k, x);
}

// k为所要移除的索引位置   x为尾结点元素
// 该方法为从删除节点向下查找
private void siftDownComparable(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>)x;
  // 中间元素，判断是否有子节点
  int half = size >>> 1;        // loop while a non-leaf
  while (k < half) {
    // 找到子节点
    int child = (k << 1) + 1; // assume left child is least
    Object c = queue[child];
    // 找到子节点的兄弟节点
    int right = child + 1;
    // 子节点和子节点的兄弟节点中找到小的
    if (right < size &&
        ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
      c = queue[child = right];
    // 尾结点元素小于子节点元素，结束循环
    if (key.compareTo((E) c) <= 0)
      break;
    // 继续向下查找
    queue[k] = c;
    k = child;
  }
  //跳出循环的条件是尾结点元素大于子节点元素了，所以将尾结点元素放到k索引位置
  queue[k] = key;
}

// k为要删除的索引位置  x为尾结点元素
private void siftUp(int k, E x) {
  if (comparator != null)
    siftUpUsingComparator(k, x);
  else
    siftUpComparable(k, x);
}

// k为要删除的索引位置  x为尾结点元素
// 从删除索引位置开始向上查找
private void siftUpComparable(int k, E x) {
  Comparable<? super E> key = (Comparable<? super E>) x;
  while (k > 0) {
    // 找到父节点
    int parent = (k - 1) >>> 1;
    Object e = queue[parent];
    // 尾结点大于父节点，直接跳出循环
    if (key.compareTo((E) e) >= 0)
      break;
    // 继续向上查找
    queue[k] = e;
    k = parent;
  }
  queue[k] = key;
}