哈夫曼树
霍夫曼树也叫哈夫曼树,也称为最优二叉树,是一种带权路径最短的二叉树。在信息检索时很常用。
概念
- 节点之间的路径长度:从一个节点到另一个节点之间的分支数量称为两个节点之间的路径长度
- 树的路径长度:从根节点到树中每一个节点的路径长度之和
- 节点的带权路径长度:从该节点到根节点之间的路径长度与节点上权的乘积
- 树的带权路径:树中所有叶子节点的带权路径长度之和
对于n个叶子节点哈夫曼树来说,一共需要2*n-1个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
| public class HuffmanTree<E> {
static class Node<E> {
E data;
double weight;
Node<E> left;
Node<E> right;
public Node(E data, double weight) {
this.data = data;
this.weight = weight;
}
@Override
public String toString() {
return new StringJoiner(", ", Node.class.getSimpleName() + "[", "]")
.add("data=" + data)
.add("weight=" + weight)
.toString();
}
}
public static void main(String[] args) {
List<Node<String>> nodes = new ArrayList<>();
nodes.add(new Node<>("A", 40));
nodes.add(new Node<>("B", 8));
nodes.add(new Node<>("C", 10));
nodes.add(new Node<>("D", 30));
nodes.add(new Node<>("E", 10));
nodes.add(new Node<>("F", 2));
Node<String> root = createTree(nodes);
System.out.println(breadthFirst(root));
}
private static <E> List<Node<E>> breadthFirst(Node root) {
Queue<Node<E>> queue = new ArrayDeque<>();
List<Node<E>> result = new ArrayList<>();
if (root != null) {
queue.add(root);
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
result.add(node);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
return result;
}
private static <E> Node<E> createTree(List<Node<E>> nodes) {
while (nodes.size() > 1) {
nodes.sort(Comparator.comparingDouble(o -> -o.weight));
Node<E> left = nodes.get(nodes.size() - 1);
Node<E> right = nodes.get(nodes.size() - 2);
Node<E> parent = new Node<E>(null, left.weight + right.weight);
parent.left = left;
parent.right = right;
nodes.remove(nodes.size() - 1);
nodes.remove(nodes.size() - 1);
nodes.add(parent);
}
return nodes.get(0);
}
}
|
结果为
1
| [Node[data=null, weight=100.0], Node[data=A, weight=40.0], Node[data=null, weight=60.0], Node[data=null, weight=30.0], Node[data=D, weight=30.0], Node[data=C, weight=10.0], Node[data=null, weight=20.0], Node[data=null, weight=10.0], Node[data=E, weight=10.0], Node[data=F, weight=2.0], Node[data=B, weight=8.0]]
|
哈夫曼编码
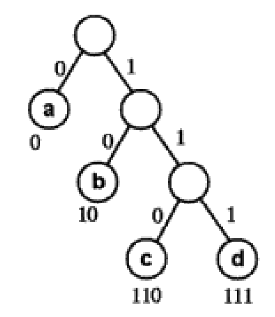
使用哈夫曼树可以解决报文编码问题,相当于进行了压缩。如对字符串”abcdabcaba”进行编码,使用频率作为权值,a、b、c、d的权值分别为4、3、2、1。从哈夫曼树根节点开始,对左子树分配代码0,对右子树分配代码1,得到的哈夫曼树为
![哈夫曼编码]()
哈夫曼编码
然后将字符串”abcdabcaba”按照该二进制码生成为0101101110101100100,仅为19个字符
v1.3.10