动态规划
还是回到贪心算法中的背包问题,使用贪心算法解决背包问题,得到的并不是最优解,而是一个近似算法。那么如何得到最优解呢,那就是动态规划。
动态规划是先解决子问题,在逐步解决大问题
- 动态规划可在给定约束条件下找到最优解
- 在问题可分解为彼此独立且离散的子问题时,可使用动态规划来解决
在动态规划中,每种动态规划解决方案都涉及到网格,每个单元格的值就是要优化的值,每个单元格都是一个子问题

背包问题
这里的计算公式为
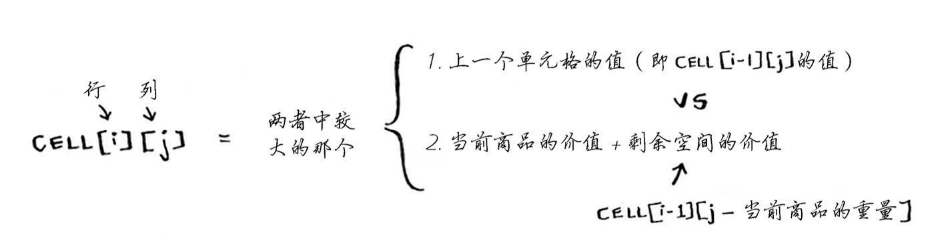
背包空闲计算公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| public class DGProblem {
public static void main(String[] args) {
int[] w = {3, 1, 4};
int[] val = {2000, 1500, 3000};
String[] names = {"笔记本电脑","吉他", "音响"};
int m = 4;
int n = val.length;
String[][] path = new String[n + 1][m + 1];
for (String[] strings : path) {
Arrays.fill(strings, "");
}
int[][] v = new int[n + 1][m + 1];
for (int i = 1; i < v.length; i++) {
for (int j = 1; j < v[0].length; j++) {
if (w[i - 1] > j) {
v[i][j] = v[i - 1][j];
path[i][j] = path[i-1][j];
} else {
if (v[i - 1][j] < (val[i - 1] + v[i - 1][j - w[i - 1]])) {
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
String goods = names[i-1]+"+"+path[i - 1][j - w[i - 1]];
path[i][j] = goods.lastIndexOf("+") == goods.length() -1 ? goods.substring(0,goods.length() -1)
: goods;
} else {
v[i][j] = v[i - 1][j];
path[i][j] = path[i-1][j];
}
}
}
}
for (int[] ints : v) {
System.out.println(Arrays.toString(ints));
}
for(int i = 1;i<path.length;i++){
for(int j = 1;j<path[i].length;j++){
System.out.print(path[i][j]+"\t\t\t");
}
System.out.println();
}
}
}
|




v1.3.10