图简介
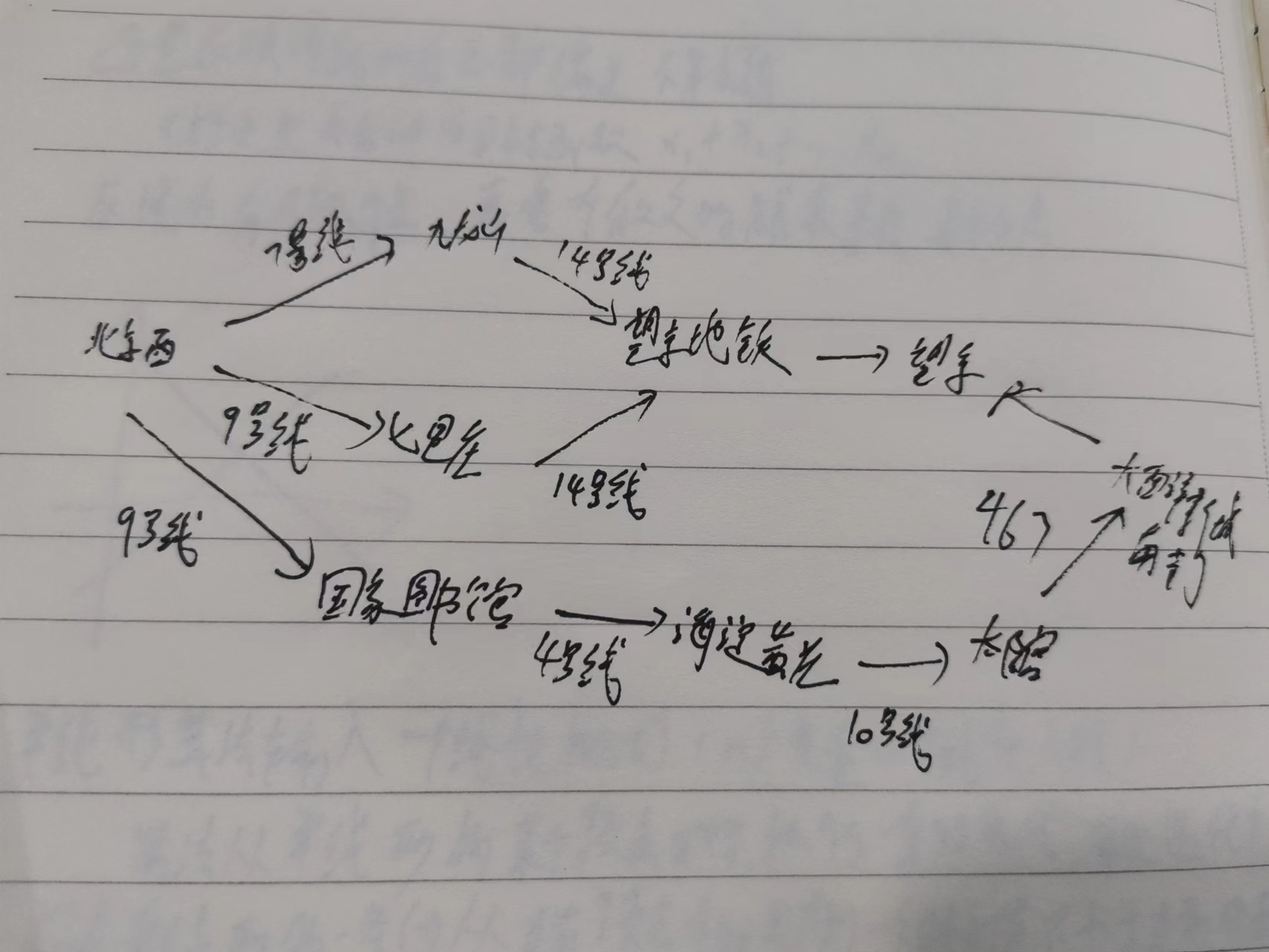
图其实我们在生活中用到的很多,比如我们要从北京西站到望京,打开高德地图,开始进行导航,会有多种方式可供选择。这就是图
![出行路线]()
要找出换乘最少的路线。这种问题被称为最短路径问题,解决最短路径问题的算法被称为广度优先算法。
什么是图
图是由节点和边组成的,一个节点可能与众多节点直接相连,这些节点被称为邻居。
有向图
顶点关系,左边起点,右边终点,所有边都有方向
无向图
没有方向
完全图
若一个无向图具有n个顶点,而每个顶点与其他n-1个顶点之间都有边,则称为无向完全图,也就是含有n个顶点的无向完全图有n(n-1)/2条边。类似的,有向图是每两个顶点之间有两条方向相反的边,也就是含有n个顶点的有向完全图有n(n-1)条边
图的存储结构
邻接矩阵
顶点之间的关系,适用稠密图存(边多)
- 无向图的是对称的,第i行(列)就是顶点的度 2e非零个数
- 有向图是不对称的,行是出度,列是入度 e个非零个数
无向图的邻接矩阵
![无向图的邻接矩阵]()
- 无向图的邻接矩阵是对称的,且主对角线元素全为0(因为自己到自己没有边)。
- 顶点i的度=第i行(列)中1的个数。
- 完全图的邻接矩阵中,主对角元素为0,其余全为1。
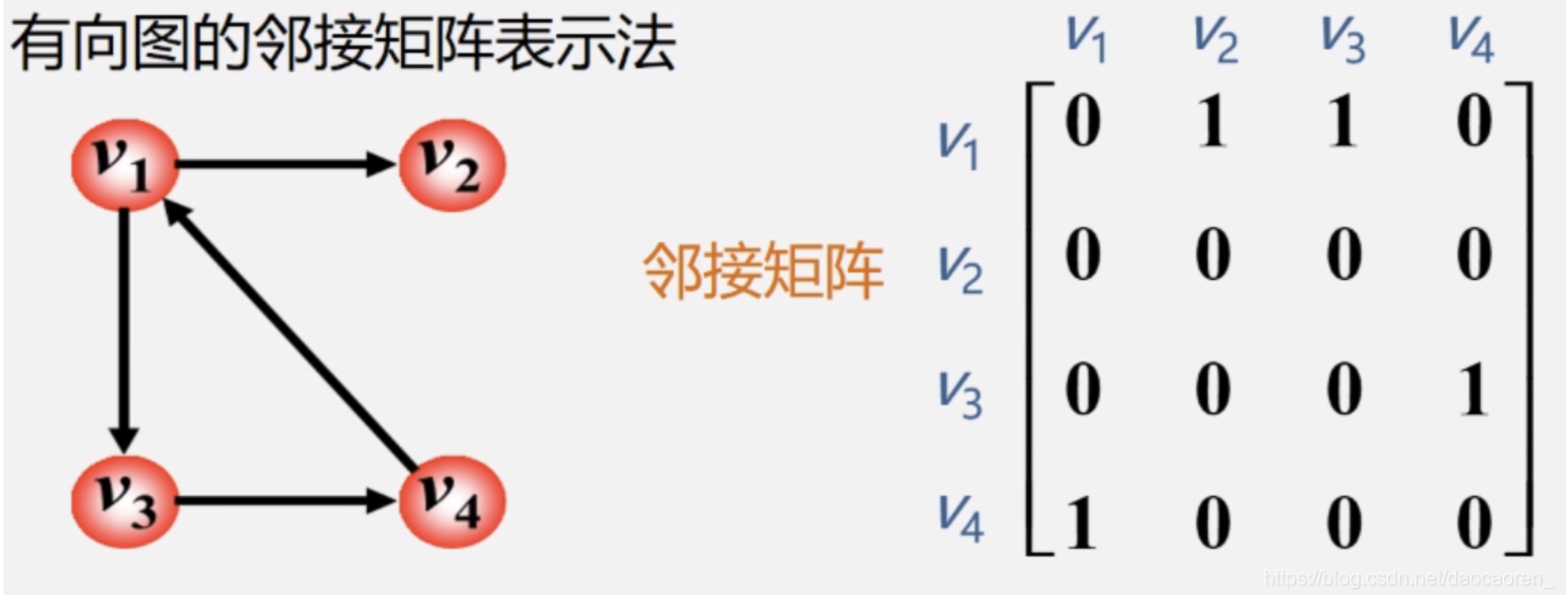
有向图的邻接矩阵
![有向图的邻接矩阵]()
- 有向图的邻接矩阵可能不是对称的。
- 顶点的出度=第i行元素之和;
顶点的入度=第i列元素之和;
顶点的度=第i行元素之和+第i列元素之和
邻接链表
- 顶点: 按编号顺序将顶点数据存储在一维数组中。
- 关联同一顶点的边: 用线性链表存储。
无向图的邻接表
![无向图邻接表]()
- 邻接表不唯一
- 若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适宜存储稀疏图。
- 无向图中顶点v${i}$的度为第i个单链表中的结点数
有向图的邻接表
![有向图的邻接表]()
- 顶点 v$i$的出度为第i个单链表中的结点个数。
- 顶点v$i$的入度为整个单链表中邻接点域值是i-1的结点个数
图的遍历
深度优先DFS
使用的是回溯的算法,对于邻接矩阵的时间复杂度是O($n^2$),对于邻接表的复杂度为O(n+e)
广度优先BFS
对于邻接矩阵的时间复杂度是O($n^2$),对于邻接表的复杂度为O(n+e)
广度优先搜索
广度优先搜索是一种用于图的查找算法,可用来解决两类问题
- 从节点A出发,是否有前往节点B的路径?
- 从节点A出发到节点B的哪条路径最短?
广度优先搜索的执行过程中,搜索范围从起点开始逐渐向外延伸。
举个在关系网中找某人的例子
比如,朋友是一度关系,朋友的朋友是二度关系。一度关系胜过二度关系,二度关系胜过三度关系。所以先在一度关系中搜索,确定其中没有老师后,才在二度关系中搜索。所以这里我们使用队列来解决这个问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
|
public class GraphSearch {
public static void main(String[] args) {
Map<String, List<String>> relationship = new HashMap<>();
init(relationship);
searchTeacher(relationship,"张思");
}
public static void searchTeacher(Map<String, List<String>> relationship,String me){
List<String> relations = relationship.get(me);
if(relations == null || relations.isEmpty()){
return;
}
Set<String> tried = new HashSet<>();
int count = 0;
Queue<String> searchQueue = new ArrayDeque<>(relations);
while (!searchQueue.isEmpty()){
String p = searchQueue.poll();
tried.add(p);
count++;
if("王燚".equals(p)){
System.out.println("找到 老师 了,找了"+count+"次");
return;
}else {
List<String> pRelations = relationship.get(p);
if(pRelations != null && pRelations.size() > 0){
for(String pp : pRelations){
if(!tried.contains(pp)){
searchQueue.add(pp);
}
}
}
}
}
System.out.println("朋友关系网中没有老师");
}
public static void init(Map<String, List<String>> relationship){
relationship.put("张玲",initP1Relation());
relationship.put("张毅",initP2Relation());
relationship.put("张二",initP3Relation());
relationship.put("张三",initP4Relation());
relationship.put("张思",initP5Relation());
}
public static List<String> initP1Relation(){
List<String> p1List = new ArrayList<>();
p1List.add("张毅");
p1List.add("张二");
p1List.add("张三");
p1List.add("张思");
p1List.add("张武");
p1List.add("张柳");
return p1List;
}
public static List<String> initP2Relation(){
List<String> p2List = new ArrayList<>();
p2List.add("张玲");
p2List.add("王燚");
p2List.add("张二");
p2List.add("王三");
p2List.add("王思");
p2List.add("王五");
return p2List;
}
public static List<String> initP3Relation(){
List<String> p3List = new ArrayList<>();
p3List.add("赵毅");
p3List.add("张玲");
p3List.add("张三");
p3List.add("张二");
p3List.add("赵武");
p3List.add("赵六");
return p3List;
}
public static List<String> initP4Relation(){
List<String> p4List = new ArrayList<>();
p4List.add("孙怡");
p4List.add("张玲");
p4List.add("张二");
p4List.add("张思");
p4List.add("孙武");
p4List.add("孙刘");
return p4List;
}
public static List<String> initP5Relation(){
List<String> p5List = new ArrayList<>();
p5List.add("张玲");
p5List.add("张三");
return p5List;
}
}
|