HashMap详解 介绍 HashMap是在项目中使用的最多的Map,实现了Map接口,继承AbstractMap。基于哈希表的Map接口实现,不包含重复的键,一个键对应一个值,在HashMap存储的时候会将key、value作为一个整体Entry进行存储。
HashMap中会根据hash算法来计算key所对应的存储位置。
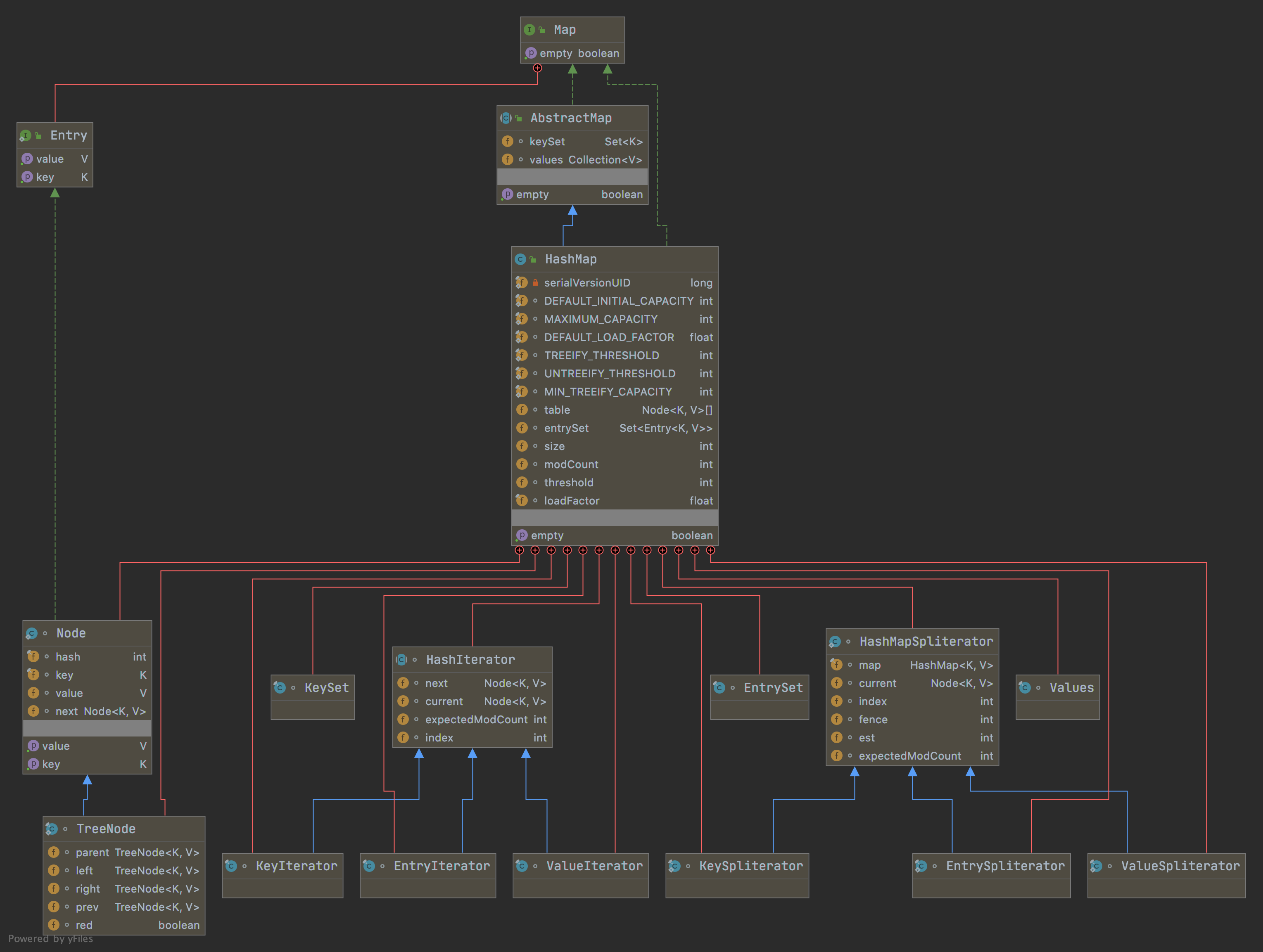
继承关系 1 2 public class HashMap <K ,V > extends AbstractMap <K ,V > implements Map <K ,V >, Cloneable , Serializable
HashMap
数据结构 数组+链表+红黑树
默认采用数组+单链表的方式存储元素,当元素出现哈希冲突时,HashMap使用链地址法来解决hash冲突,会存储在该位置的链表中。当链表中元素个数超过8个时,会尝试将链表转为红黑树存储。但是在转换前,会判断一次当前数组的长度,当数组长度大于64时才会处理,否则进行扩容操作
源码解析 重要参数 初始大小和加载因子
静态常量 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4 ; static final int MAXIMUM_CAPACITY = 1 << 30 ;static final float DEFAULT_LOAD_FACTOR = 0.75f ;static final int TREEIFY_THRESHOLD = 8 ;static final int UNTREEIFY_THRESHOLD = 6 ;static final int MIN_TREEIFY_CAPACITY = 64 ;
为什么容量一定要是2次幂
在计算数组下标时使用的是(n - 1) & hash来计算的,当n为2次幂时,n-1的低位将全是1,哈希值进行与操作时保证低位不变,最终得到的index结果,完全取决于key的hashCode的最后几位,从而保证分布均匀,效果等同于取模,且性能比取模高。
Node HashMap中的元素都存储在Node数组中,看一下Node的结构
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 transient Node<K,V>[] table;static class Node <K ,V > implements Map .Entry <K ,V > final int hash; final K key; V value; Node<K,V> next; Node(int hash, K key, V value, Node<K,V> next) { this .hash = hash; this .key = key; this .value = value; this .next = next; } public final K getKey () return key; } public final V getValue () return value; } public final String toString () return key + "=" + value; } public final int hashCode () return Objects.hashCode(key) ^ Objects.hashCode(value); } public final V setValue (V newValue) V oldValue = value; value = newValue; return oldValue; } public final boolean equals (Object o) if (o == this ) return true ; if (o instanceof Map.Entry) { Map.Entry<?,?> e = (Map.Entry<?,?>)o; if (Objects.equals(key, e.getKey()) && Objects.equals(value, e.getValue())) return true ; } return false ; } }
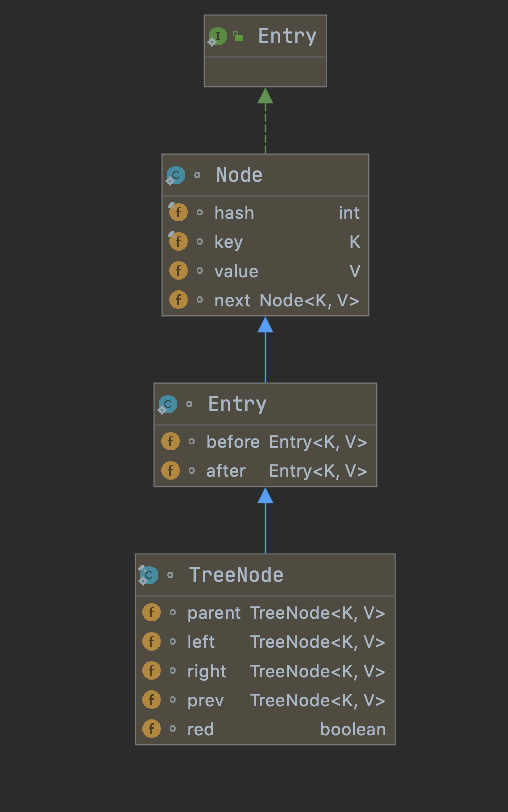
Node
如果是链表,则使用的是Node存储(单向链表);如果是红黑树,则使用的是TreeNode
构造函数 无参构造函数 1 2 3 public HashMap () this .loadFactor = DEFAULT_LOAD_FACTOR; }
指定初始容量 1 2 3 public HashMap (int initialCapacity) this (initialCapacity, DEFAULT_LOAD_FACTOR); }
指定初始容量和加载因子 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public HashMap (int initialCapacity, float loadFactor) if (initialCapacity < 0 ) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); this .loadFactor = loadFactor; this .threshold = tableSizeFor(initialCapacity); } static final int tableSizeFor (int cap) int n = cap - 1 ; n |= n >>> 1 ; n |= n >>> 2 ; n |= n >>> 4 ; n |= n >>> 8 ; n |= n >>> 16 ; return (n < 0 ) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1 ; }
传入map 1 2 3 4 public HashMap (Map<? extends K, ? extends V> m) this .loadFactor = DEFAULT_LOAD_FACTOR; putMapEntries(m, false ); }
方法分析 put方法添加元素 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public V put (K key, V value) return putVal(hash(key), key, value, false , true ); } static final int hash (Object key) int h; return (key == null ) ? 0 : (h = key.hashCode()) ^ (h >>> 16 ); } final V putVal (int hash, K key, V value, boolean onlyIfAbsent, boolean evict) Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0 ) n = (tab = resize()).length; if ((p = tab[i = (n - 1 ) & hash]) == null ) tab[i] = newNode(hash, key, value, null ); else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this , tab, hash, key, value); else { for (int binCount = 0 ; ; ++binCount) { if ((e = p.next) == null ) { p.next = newNode(hash, key, value, null ); if (binCount >= TREEIFY_THRESHOLD - 1 ) treeifyBin(tab, hash); break ; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break ; p = e; } } if (e != null ) { V oldValue = e.value; if (!onlyIfAbsent || oldValue == null ) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) resize(); afterNodeInsertion(evict); return null ; }
两个key对象hash值相同就会发生hash碰撞,此时就会将Node插入链表中(JDK7采用头插法,JDK8采用尾插法)
扩容 当hashMap中的容量达到阈值时,就会开始扩容操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 final Node<K,V>[] resize() { Node<K,V>[] oldTab = table; int oldCap = (oldTab == null ) ? 0 : oldTab.length; int oldThr = threshold; int newCap, newThr = 0 ; if (oldCap > 0 ) { if (oldCap >= MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE; return oldTab; } else if ((newCap = oldCap << 1 ) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) newThr = oldThr << 1 ; } else if (oldThr > 0 ) newCap = oldThr; else { newCap = DEFAULT_INITIAL_CAPACITY; newThr = (int )(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); } if (newThr == 0 ) { float ft = (float )newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float )MAXIMUM_CAPACITY ? (int )ft : Integer.MAX_VALUE); } threshold = newThr; @SuppressWarnings({"rawtypes","unchecked"}) Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; if (oldTab != null ) { for (int j = 0 ; j < oldCap; ++j) { Node<K,V> e; if ((e = oldTab[j]) != null ) { oldTab[j] = null ; if (e.next == null ) newTab[e.hash & (newCap - 1 )] = e; else if (e instanceof TreeNode) ((TreeNode<K,V>)e).split(this , newTab, j, oldCap); else { Node<K,V> loHead = null , loTail = null ; Node<K,V> hiHead = null , hiTail = null ; Node<K,V> next; do { next = e.next; if ((e.hash & oldCap) == 0 ) { if (loTail == null ) loHead = e; else loTail.next = e; loTail = e; } else { if (hiTail == null ) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null ); if (loTail != null ) { loTail.next = null ; newTab[j] = loHead; } if (hiTail != null ) { hiTail.next = null ; newTab[j + oldCap] = hiHead; } } } } } return newTab; }
红黑树转换 将单向链表转为双向链表,再遍历双向链表转为红黑树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 final void treeifyBin (Node<K,V>[] tab, int hash) int n, index; Node<K,V> e; if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize(); else if ((e = tab[index = (n - 1 ) & hash]) != null ) { TreeNode<K,V> hd = null , tl = null ; do { TreeNode<K,V> p = replacementTreeNode(e, null ); if (tl == null ) hd = p; else { p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null ); if ((tab[index] = hd) != null ) hd.treeify(tab); } }
双向链表转为红黑树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 final void treeify (Node<K,V>[] tab) TreeNode<K,V> root = null ; for (TreeNode<K,V> x = this , next; x != null ; x = next) { next = (TreeNode<K,V>)x.next; x.left = x.right = null ; if (root == null ) { x.parent = null ; x.red = false ; root = x; } else { K k = x.key; int h = x.hash; Class<?> kc = null ; for (TreeNode<K,V> p = root;;) { int dir, ph; K pk = p.key; if ((ph = p.hash) > h) dir = -1 ; else if (ph < h) dir = 1 ; else if ((kc == null && (kc = comparableClassFor(k)) == null ) || (dir = compareComparables(kc, k, pk)) == 0 ) dir = tieBreakOrder(k, pk); TreeNode<K,V> xp = p; if ((p = (dir <= 0 ) ? p.left : p.right) == null ) { x.parent = xp; if (dir <= 0 ) xp.left = x; else xp.right = x; root = balanceInsertion(root, x); break ; } } } } moveRootToFront(tab, root); }
将红黑树的根节点移动到数组的索引所在位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 static <K,V> void moveRootToFront (Node<K,V>[] tab, TreeNode<K,V> root) int n; if (root != null && tab != null && (n = tab.length) > 0 ) { int index = (n - 1 ) & root.hash; TreeNode<K,V> first = (TreeNode<K,V>)tab[index]; if (root != first) { Node<K,V> rn; tab[index] = root; TreeNode<K,V> rp = root.prev; if ((rn = root.next) != null ) ((TreeNode<K,V>)rn).prev = rp; if (rp != null ) rp.next = rn; if (first != null ) first.prev = root; root.next = first; root.prev = null ; } assert checkInvariants (root) } }
使用红黑树是因为二叉树在特殊情况下会变成线性结构,导致遍历依然很慢,而红黑树插入数据会通过左旋、右旋、变色操作来保持平衡
红黑树插入 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 final TreeNode<K,V> putTreeVal (HashMap<K,V> map, Node<K,V>[] tab, int h, K k, V v) Class<?> kc = null ; boolean searched = false ; TreeNode<K,V> root = (parent != null ) ? root() : this ; for (TreeNode<K,V> p = root;;) { int dir, ph; K pk; if ((ph = p.hash) > h) dir = -1 ; else if (ph < h) dir = 1 ; else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; else if ((kc == null && (kc = comparableClassFor(k)) == null ) || (dir = compareComparables(kc, k, pk)) == 0 ) { if (!searched) { TreeNode<K,V> q, ch; searched = true ; if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null ) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null )) return q; } dir = tieBreakOrder(k, pk); } TreeNode<K,V> xp = p; if ((p = (dir <= 0 ) ? p.left : p.right) == null ) { Node<K,V> xpn = xp.next; TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); if (dir <= 0 ) xp.left = x; else xp.right = x; xp.next = x; x.parent = x.prev = xp; if (xpn != null ) ((TreeNode<K,V>)xpn).prev = x; moveRootToFront(tab, balanceInsertion(root, x)); return null ; } } }
红黑树拆分 在进行扩容操作时,会重新计算索引位置,拆分之后的红黑树需要判断个数,从而决定做去树化还是树化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 final void split (HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) TreeNode<K,V> b = this ; TreeNode<K,V> loHead = null , loTail = null ; TreeNode<K,V> hiHead = null , hiTail = null ; int lc = 0 , hc = 0 ; for (TreeNode<K,V> e = b, next; e != null ; e = next) { next = (TreeNode<K,V>)e.next; e.next = null ; if ((e.hash & bit) == 0 ) { if ((e.prev = loTail) == null ) loHead = e; else loTail.next = e; loTail = e; ++lc; } else { if ((e.prev = hiTail) == null ) hiHead = e; else hiTail.next = e; hiTail = e; ++hc; } } if (loHead != null ) { if (lc <= UNTREEIFY_THRESHOLD) tab[index] = loHead.untreeify(map); else { tab[index] = loHead; if (hiHead != null ) loHead.treeify(tab); } } if (hiHead != null ) { if (hc <= UNTREEIFY_THRESHOLD) tab[index + bit] = hiHead.untreeify(map); else { tab[index + bit] = hiHead; if (loHead != null ) hiHead.treeify(tab); } } }
去树化操作 1 2 3 4 5 6 7 8 9 10 11 12 final Node<K,V> untreeify (HashMap<K,V> map) Node<K,V> hd = null , tl = null ; for (Node<K,V> q = this ; q != null ; q = q.next) { Node<K,V> p = map.replacementNode(q, null ); if (tl == null ) hd = p; else tl.next = p; tl = p; } return hd; }
put操作的大致步骤如下:
对key进行hash操作,找到索引位置,如果此时索引位置为null,直接插入
如果此时索引位置不为null,说明出现了hash冲突,使用equals()比较key的值,如果存在与该key相同的值,则替换value
如果不存在与该key相同的值,且此时存储结构为链表,则插入链表尾部,如果链表长度超过8个且数组长度大于64时,进行链表转红黑树
当数组中数据达到阈值,则需要进行扩容,扩容时需要进行去树化
get方法获取元素 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public V get (Object key) Node<K,V> e; return (e = getNode(hash(key), key)) == null ? null : e.value; } final Node<K,V> getNode (int hash, Object key) Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1 ) & hash]) != null ) { if (first.hash == hash && ((k = first.key) == key || (key != null && key.equals(k)))) return first; if ((e = first.next) != null ) { if (first instanceof TreeNode) return ((TreeNode<K,V>)first).getTreeNode(hash, key); do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null ); } } return null ; }
高并发问题 由于HashMap不是线程安全的,在高并发的情况下会出现问题,在插入时可能会出现问题
1.7时的问题 假如HashMap到达了扩容的临界点,此时有两个线程在同一时刻对HashMap进行put操作,两个线程都会进行扩容可能会形成链表环,一旦形成环形数据结构,Entry的next节点永远不为空,使得下一次读操作出现死循环
1.8时的问题 两个线程都进入put操作,并且计算的下标相同,会导致两个线程设置的数据被覆盖
v1.3.10