查找算法
线性查找
顺序查找
按照顺序遍历与所查找的数进行比较
1
2
3
4
5
6
7
| public static int search(int[] arry, int des) {
for (int i = 0; i <= arry.length - 1; i++) {
if (des == arry[i])
return i;
}
return -1;
}
|
查找的时间复杂度为N,插入的时间复杂度为N
二分查找
二分查找要求元素必须是有顺序的,每次中间值与所要查找的数进行比较,如果要找的元素值小于中间值,则将待查序列缩小为左半部分,否则为右半部分,通过一次比较,将查找区间缩小一半
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public static int search(int[] arr,int des){
int start = 0;
int end = arr.length - 1;
while (start <= end){
int mid = (start + end )/2;
if(arr[mid] == des){
return mid;
} else if(arr[mid] > des){
end = mid - 1;
} else {
start = mid + 1;
}
}
return -1;
}
|
查找的时间复杂度为 ,插入的时间复杂度为
分块查找
分块查找是顺序查找和二分查找的整合,把一个大的线性表分为若干块,每块中找到一个最大值以及起始索引组成索引表,要求索引表是有序的,块与块之间需要排序,而对于每块内的节点没有排序要求
查找树
二叉查找树
二叉查找树的特点
- 每个节点只能有一个父节点指向自己(除根节点外,根节点没有父节点)
- 若它的左子树不空,则其左子树中所有节点的值不大于根节点的值
- 若它的右子树不空,则其右子树中所有节点的值不小于根节点的值
- 它的左右子树都是二叉查找树
使用二叉查找树来进行查找的方法是从根节点开始,递归的缩小查找范围,待查关键字与根节点元素关键字比较,若相等则返回根节点;若待查关键字小,则递归的在查找树的左子树中查找,否则递归在查找树的右子树中查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| public static class BST<K extends Comparable, V> {
private Node root;
private class Node {
private K key;
private V value;
private Node left, right;
private int N;
public Node(K key, V value, int n) {
this.key = key;
this.value = value;
N = n;
}
}
public int size() {
return size(root);
}
private int size(Node node) {
if (node == null)
return 0;
else
return node.N;
}
public V get(K key) {
if(key == null)
throw new RuntimeException("不允许为空");
return get(root, key);
}
private V get(Node node, K key) {
if (node == null)
throw new RuntimeException("不允许为空");
int cmp = key.compareTo(node.key);
if (cmp < 0)
return get(node.left, key);
else if (cmp > 0)
return get(node.right, key);
else return node.value;
}
public void put(K key, V value) {
if(key == null)
throw new RuntimeException("不允许为空");
root = put(root, key, value);
}
private Node put(Node node, K key, V value) {
if (node == null)
return new Node(key, value, 1);
int cmp = key.compareTo(node.key);
if (cmp < 0)
node.left = put(node.left, key, value);
else if (cmp > 0)
node.right = put(node.right, key, value);
else
node.value = value;
node.N = size(node.left) + size(node.right) + 1;
return node;
}
}
|
查找的时间复杂度为N,插入的时间复杂度为N
平衡二叉树(AVL)
二叉查找树的高度直接影响了各操作的性能,而且在某些特殊的情况下二叉查找树回退化为一个单链表,所以又提出了一个平衡二叉树的概念,其二叉树的所有节点的左右子树的高度差的绝对值不差过1则称为平衡二叉树
在对一个平衡二叉树进行插入或删除操作时,可能会使得其不再满足平衡二叉树的条件,此时需要调整其结构使其重新平衡
旋转操作
旋转分为右旋和左旋
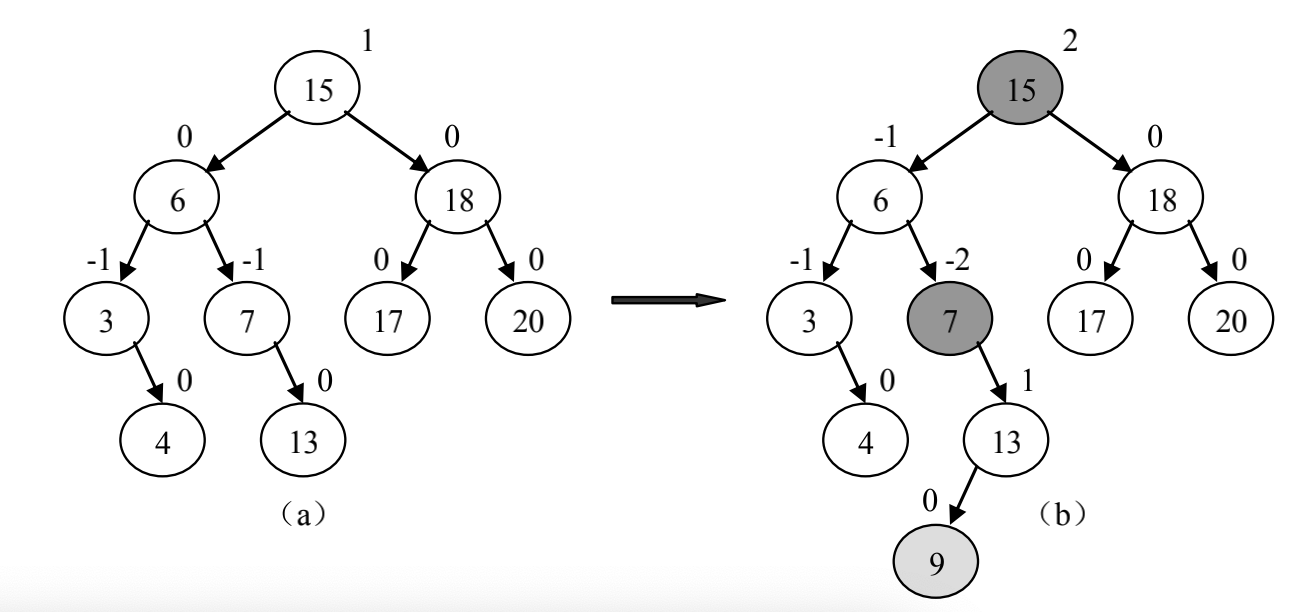
![平衡二叉树]()
平衡二叉树
在插入新的节点x之后平衡二叉树失去平衡,则失去平衡的节点只可能是x的祖先,且层次数小于等于x的祖父的节点,也就是说失去平衡的节点时从x的祖父到根路径上的节点,但是这些节点并不都是失去平衡的点,有些节点可能仍然是平衡的
为了使之再次平衡,可以从节点x出发逆行向上,依次检查x祖先的平衡因子,找到第一个失衡的祖先节点g,在从x到g的路径上,假设p为g的孩子节点,v为p的孩子节点,其有四种组合方式
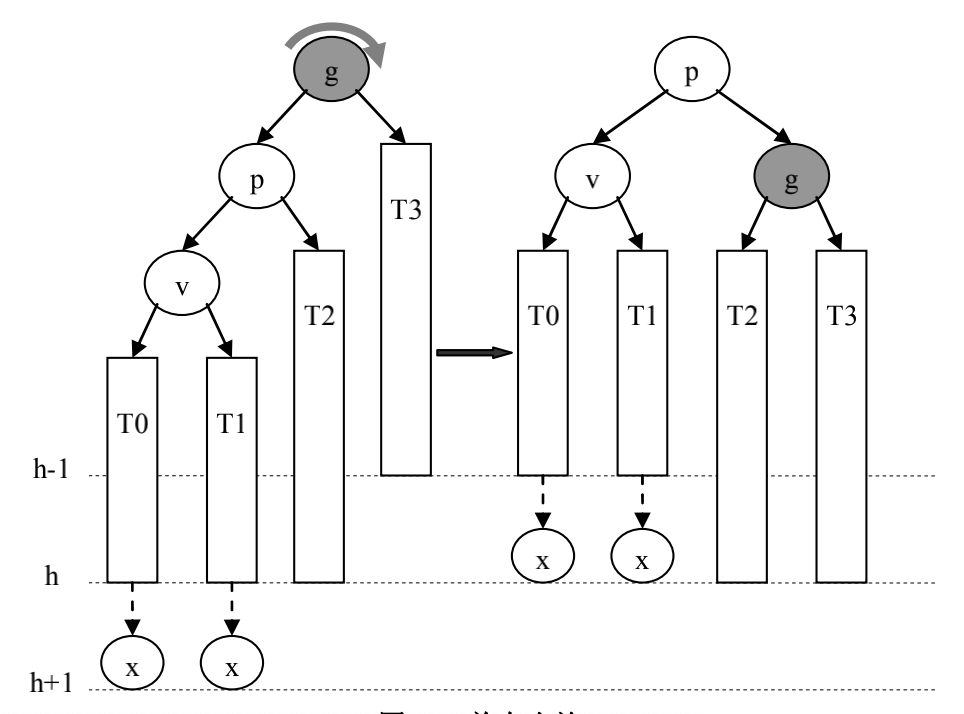
p是g的左孩子,且v是p的左孩子(失衡是由于g的左子树过高导致的)
可通过节点g的单向右旋,使得以g为根的子树得到平衡
![单向右旋]()
单向右旋
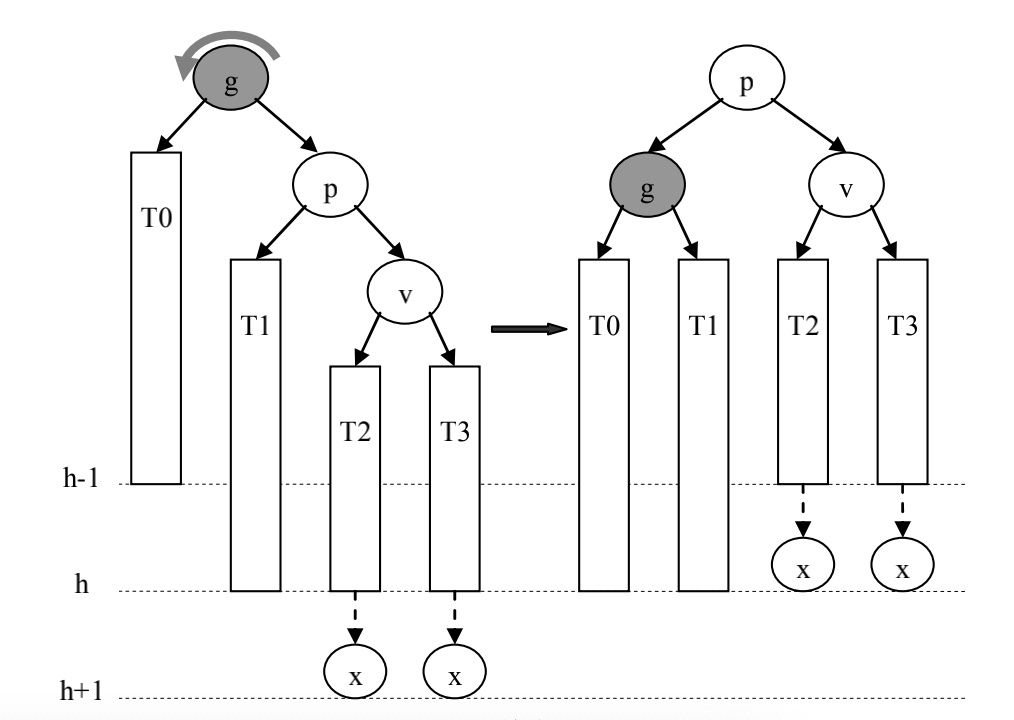
p是g的右孩子,且v是p的右孩子(失衡是由于g的右子树过高导致的)
可通过节点g的单向左旋来完成局部的平衡
![单向左旋]()
单向左旋
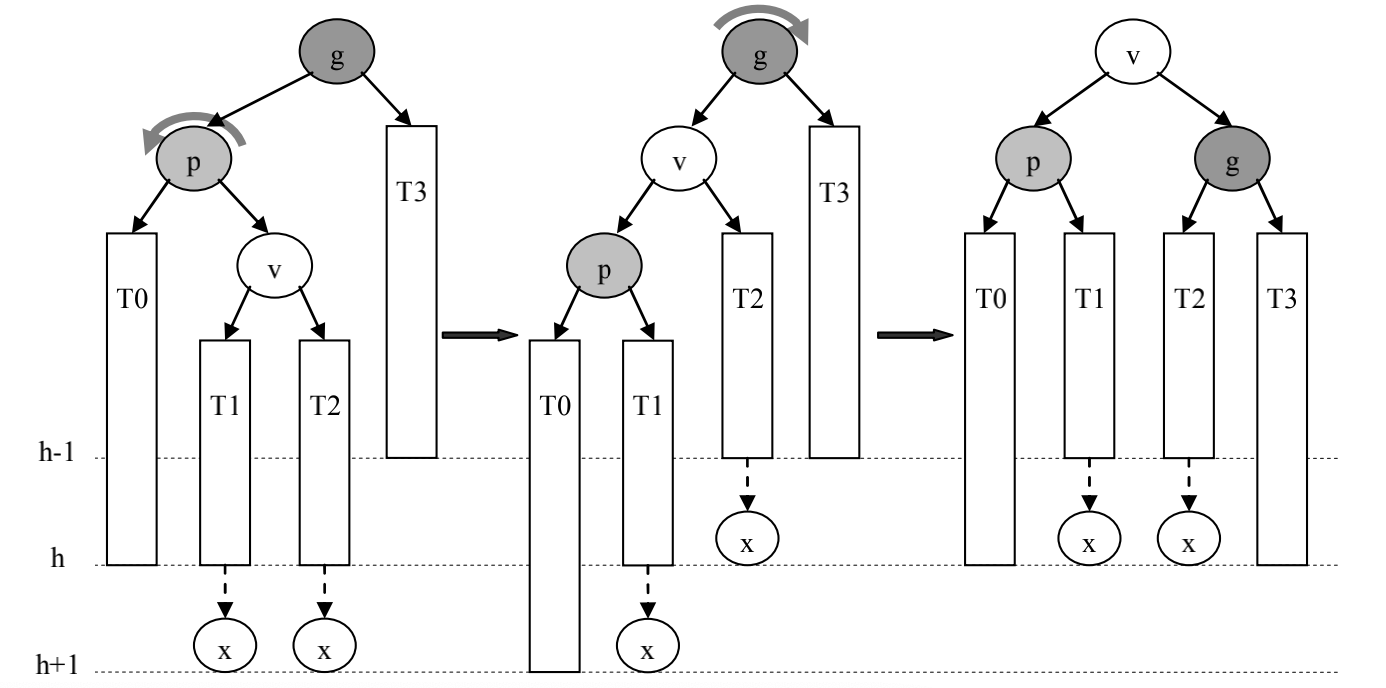
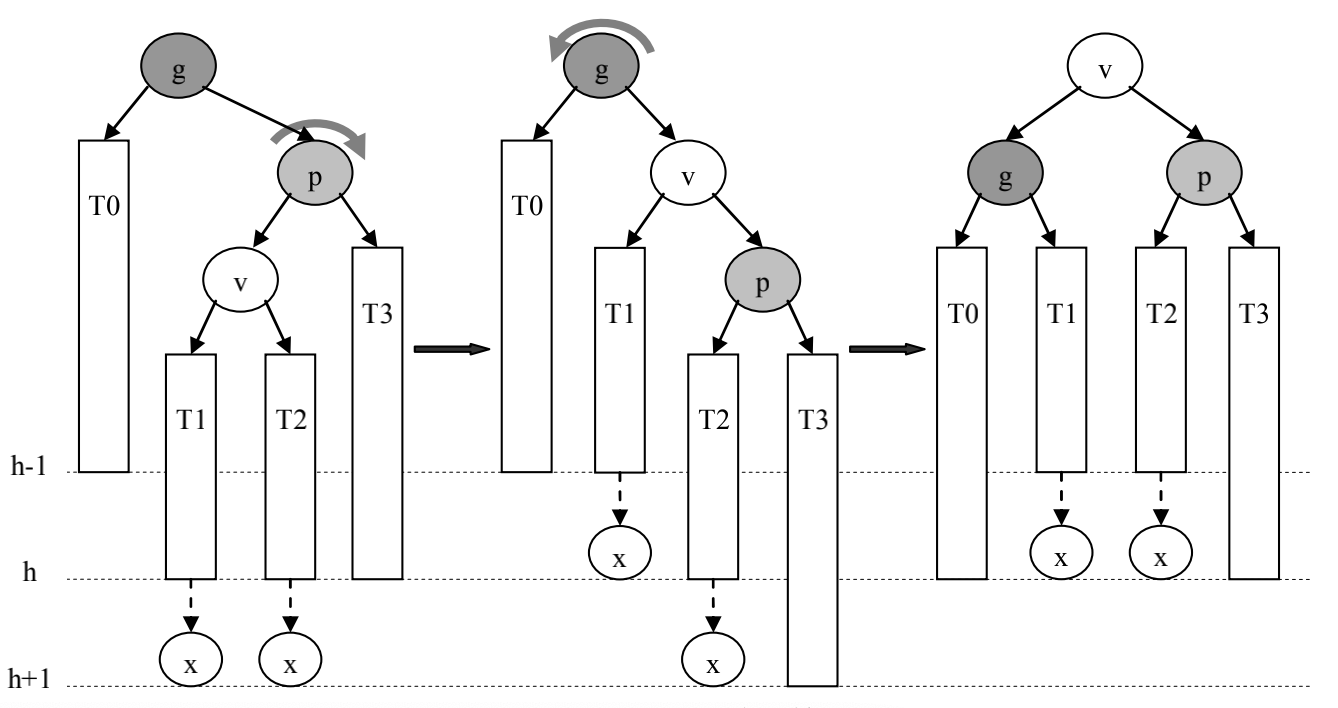
p是g的左孩子,且v是p的右孩子(失衡是由于g的左孩子的右子树过高导致的)
先对p进行左旋,再对g进行右旋
![先左旋后右旋]()
先左旋后右旋
p是g的右孩子,且v是p的左孩子(失衡是由于g的右孩子的左子树过高导致的)
先对p进行右旋,再对g进行左旋
![先右旋后左旋]()
先右旋后左旋
哈希查找
使用哈希查找的算法分为两步:第一步是用哈希函数将被查找的键转化为数组的一个索引;第二步是处理哈希碰撞冲突,如使用拉链法或者线性探测法
v1.3.10