树简介
树跟数组、链表、堆栈一样,是一种数据结构。它由有限个节点,组成具有层次关系的集合
- 节点的度:一个节点含有的子节点个数称为该节点的度;
- 树的度:一棵树中,最大节点的度称为树的度;
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 叶子节点:节点的度为0;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根节点的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0
特点
- 每个节点或者无子节点或者只有有限个子节点;
- 有一个特殊的节点,它没有父节点,称为根节点;
- 每一个非根节点有且只有一个父节点;
- 树里面没有环路
树的遍历
- 前序遍历DLR:遍历顺序为 根节点->左子树->右子树
- 中序遍历LDR:遍历顺序为 左子树->根节点->右子树
- 后序遍历LRD:遍历顺序为 左子树->右子树->根节点
分类
按照有序性,可以分为有序树和无序树:
- 无序树:树中任意节点的子节点之间没有顺序关系
- 有序树:树中任意节点的子节点之间有顺序关系
按照节点包含子树个数,可以分为B树和二叉树,
二叉树
左子树和右子树都为空的元素称为叶节点
二叉树可以分为以下几种:
二叉树:每个节点最多含有两个子树的树称为二叉树;
二叉查找树(BST):首先它是一颗二叉树,若左子树不空,则左子树上所有节点的值均小于它的根节点的值;若右子树不空,则右子树上所有节点的值均大于它的根节点的值;左、右子树也分别为二叉排序树;
极端情况下会退化为链表
满二叉树:叶节点除外的所有节点均含有两个子树的树被称为满二叉树;
完全二叉树:如果一颗二叉树除去最后一层节点为满二叉树,且最后一层的节点依次从左到右分布
霍夫曼树:带权路径最短的二叉树,又称最优二叉树。
红黑树:红黑树是一颗特殊的二叉查找树,每个节点都是黑色或者红色,根节点、叶子节点是黑色。如果一个节点是红色的,则它的子节点必须是黑色的,且从根节点到某个无子节点或者只有一个子节点的元素的所有路径中,黑色元素的数量必须相同
通过引入红黑节点,舍弃了AVL严格的平衡,旋转次数会有所减少,但是由于二叉树可能数比较高,IO次数比较多,所以在磁盘场景中会使用B树
平衡二叉树(AVL):符合二叉查找树的定义,且满足一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,通过左旋和右旋来得到插入或更新后树的平衡性
旋转比较耗时,删除数据时效率比较低,再删除操作较多时,性能可能会比较差,所以用红黑树比用AVL多
B树
B树的定义和操作是很复杂的,是为磁盘场景设计的多路平衡查找树,每个非叶节点可以有多个子树。因此在总结点数量相同时,B树的高度远远小于AVL树和红黑树,大大减少了磁盘IO次数
通过将二叉树改为多路平衡查找树,解决了树高的问题
B+树
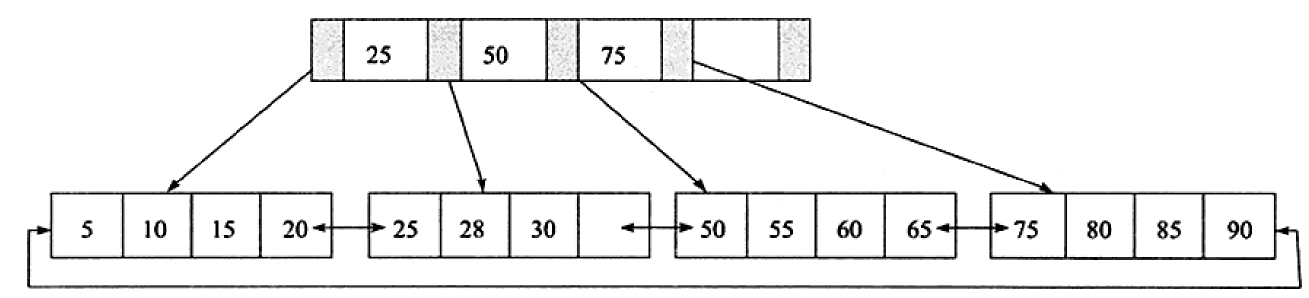
B+树中,所有记录节点都是按照键值的大小顺序存放在同一层的叶子节点上,由各叶子节点指针进行连接
B+树的插入必须保证插入后叶子节点中的记录依然有序,同时需要考虑插入到B+树的三种情况
情况一:Leaf Page没满,Index page没满
此时可以直接将记录插入到叶子节点
情况二:Leaf Page满,Index page没满
此时需要拆分Leaf Page,将中间的节点放入到Index page中,小于中间节点的记录放在左边,大于或等于中间节点的记录放在右边
情况三:Leaf Page满,Index page满
此时需要拆分Leaf Page,小于中间节点的记录放左边,大于或等于中间节点的记录放右边,拆分Index Page,小于中间节点的记录放左边,大于中间节点的记录方右边,中间节点放入上一层Index page
因为B+树结构主要用于磁盘,页的拆分意味着磁盘的操作,所以应该尽可能的减少页的拆分操作,所以B+树也同样提供了平衡二叉树的旋转操作,当Leaf Page满,但是其兄弟节点没有满的情况下,此时B+树不会急于去做拆分页的操作,而是将记录移到页的兄弟节点上,通常情况下,左兄弟会被首先检查用来用来做旋转操作
B+树使用填充因子(最小值是50%)来控制树的删除变化,且同样需要保证删除后叶子节点中的记录依然有序,也需要考虑三种情况
情况一:叶子节点不小于填充因子,中间节点不小于填充因子
此时可以直接将记录从叶子节点删除,如果该节点还是Index Page的节点,用该节点的右节点代替
情况二:叶子节点小于填充因子,中间节点不小于填充因子
此时需要合并叶子节点和它的兄弟节点,同时更新Index page
情况三:叶子节点小于填充因子,中间节点小于填充因子
此时需要合并叶子节点和它的兄弟节点,更新Index page,合并Index page和它的兄弟节点